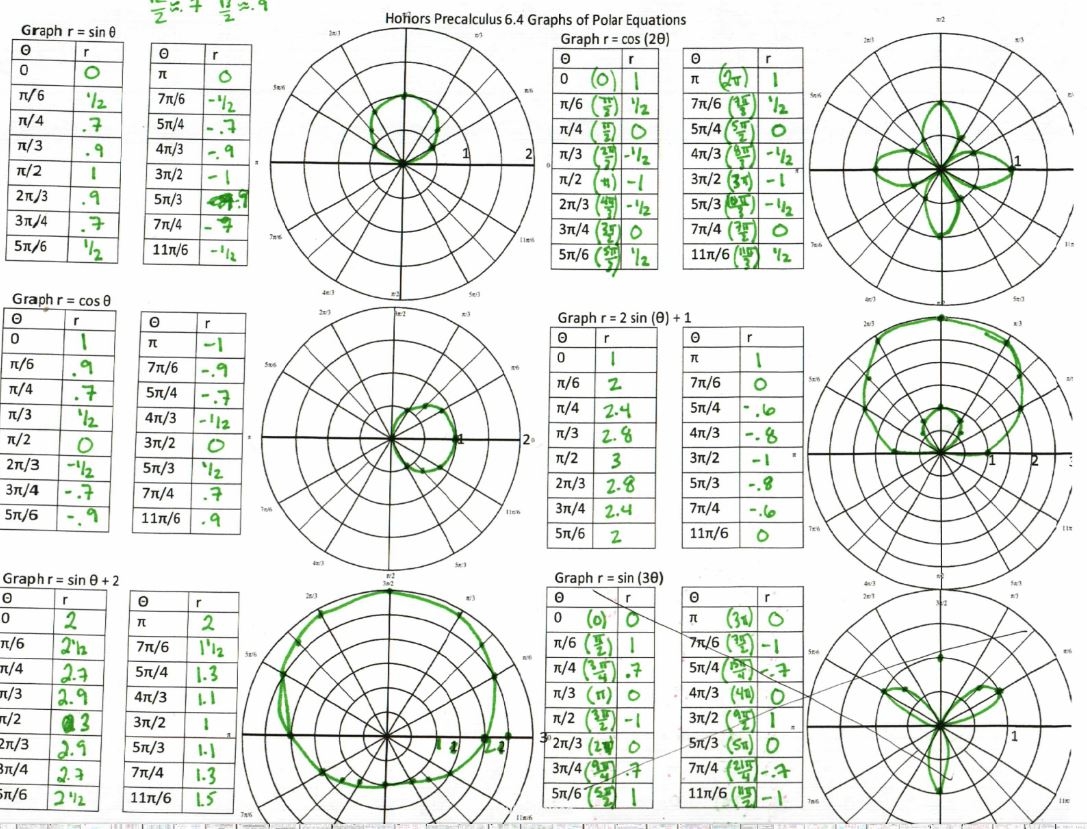
Polar equations are a unique way to represent mathematical functions using polar coordinates. These equations are often used in physics, engineering, and other fields to describe complex patterns and shapes. Graphing polar equations can provide insight into the behavior of these functions and help visualize their geometric properties.
One common application of polar equations is finding the area enclosed by a polar curve. This involves calculating the area of the region bounded by the curve and the origin. By integrating the polar equation over a specified interval, it is possible to determine the area of the enclosed region.
Graph and Find Area of Polar Equations Worksheet
When working with polar equations, it is important to understand how to graph these functions and calculate the area enclosed by them. A worksheet on graphing and finding the area of polar equations can help reinforce these concepts and provide practice for students. The worksheet may include a variety of polar equations for students to graph and find the area of, as well as guided questions to help them understand the process.
One approach to graphing polar equations is to convert them to rectangular form using trigonometric identities. This can make it easier to plot the points and visualize the curve. Once the curve is graphed, students can determine the area enclosed by the curve by integrating the equation over a specified interval. This process involves calculating the area of each sector and summing them to find the total enclosed area.
Another method for finding the area of a polar curve is to use the formula for the area of a sector of a circle. By dividing the curve into small sectors and summing their areas, students can approximate the total enclosed area. This method can be useful for complex curves where integration may be challenging.
Overall, graphing and finding the area of polar equations can be a challenging but rewarding exercise for students. By practicing these skills on a worksheet, students can improve their understanding of polar coordinates and develop their problem-solving abilities. Additionally, working with polar equations can help students appreciate the beauty and elegance of mathematical functions in a new light.
In conclusion, graphing and finding the area of polar equations is a valuable skill for students to develop. A worksheet on this topic can provide practice and reinforcement of these concepts, helping students build their confidence and proficiency in working with polar coordinates. By mastering these skills, students can deepen their understanding of mathematical functions and their applications in various fields.